Block Coding Techniques in Error Detection and Correction
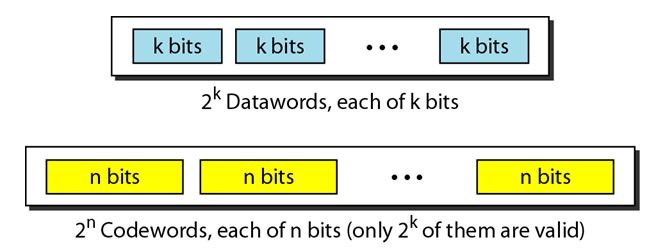
In block coding, we divide our message into blocks, each of k bits, called data words. We add r redundant bits to each block to make the length n = k + r. The resulting n-bit blocks are called code words.
For example, we have a set of data words, each of size k, and a set of code words, each of size of n. With k bits, we can create a combination of 2k data words, with n bits; we can create a combination of 2n code words. Since n > k, the number of possible code words is larger than the number of possible data words.
The block coding process is one-to-one; the same data word is always encoded as the same code word. This means that we have 2n-2k code words that are not used. We call these code words invalid or illegal. The following figure shows the situation.
Error Detection
If the following two conditions are met, the receiver can detect a change in the original code word by using Block coding technique.
1. The receiver has (or can find) a list of valid code words.
2. The original code word has changed to an invalid one.
The sender creates code words out of data words by using a generator that applies the rules and procedures of encoding (discussed later). Each code word sent to the receiver may change during transmission. If the received code word is the same as one of the valid code words, the word is accepted; the corresponding data word is extracted for use.
You May Also Like:
Types of Errors
Important Concepts in Error Detection and Correction
Hamming Distance
If the received code word is not valid, it is discarded. However, if the code word is corrupted during transmission but the received word still matches a valid code word, the error remains undetected. This type of coding can detect only single errors. Two or more errors may remain undetected.
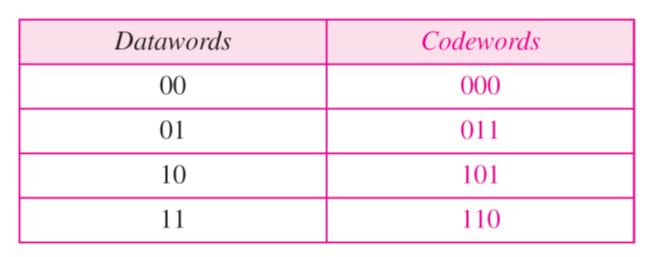
For example consider the following table of data words and Code words:
Assume the sender encodes the data word 01 as 011 and sends it to the receiver. Consider the following cases:
1. The receiver receives O11. It is a valid code word. The receiver extracts the data word 01 from it.
2. The code word is corrupted during transmission, and 111 is received (the leftmost bit is corrupted). This is not a valid code word and is discarded.
3. The code word is corrupted during transmission, and 000 is received (the right two bits are corrupted). This is a valid code word. The receiver incorrectly extracts the data word 00. Two corrupted bits have made the error undetectable.
Error Correction:
Error correction is much more difficult than error detection. In error detection, the receiver needs to know only that the received code word is invalid, in error correction the receiver needs to find (or guess) the original code word sent. So, we need more redundant bits for error correction than for error detection.
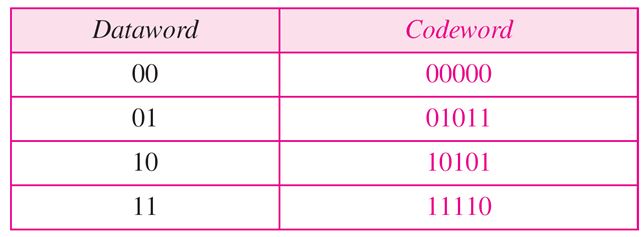
Consider the following table of Data words and Code words.
Assume the data word is 01. The sender consults the table (or uses an algorithm) to create the code word 01011. The code word is corrupted during transmission, and 01001 is received (error in the second bit from the right). First, the receiver finds that the received code word is not in the table. This means an error has occurred. (Detection must come before correction.) The receiver, assuming that there is only 1 bit corrupted, uses the following strategy to guess the correct data word.
1. Comparing the received code word with the first code word in the table (01001 versus 00000), the receiver decides that the first code word is not the one that was sent because there are two different bits.
2. By the same reasoning, the original code word cannot be the third or fourth one in the table.
3. The original code word must be the second one in the table because this is the only one that differs from the received code word by 1 bit. The receiver replaces 01001 with 01011 and consults the table to find the data word 01.
You May Also Like:
Simple Parity Check Code
Hamming Codes
Cyclic Codes
C hecksum
Back to DCN Questions and Answers